Mathematical Physics - Quantum-Relativity (qr)
qr forces us to face up to a great misunderstanding and error that has become embedded within mankind's deeply flawed additive-led or flat understanding of Nature's multiplicative-led exponential or curved mathematical logic.
I will start explaining qr-math by clarifying the exponential relationship between two well-known numbers; +1 and -1.
Please note that "anti-logarithm" is the common or popular name for the reverse exponential transform.
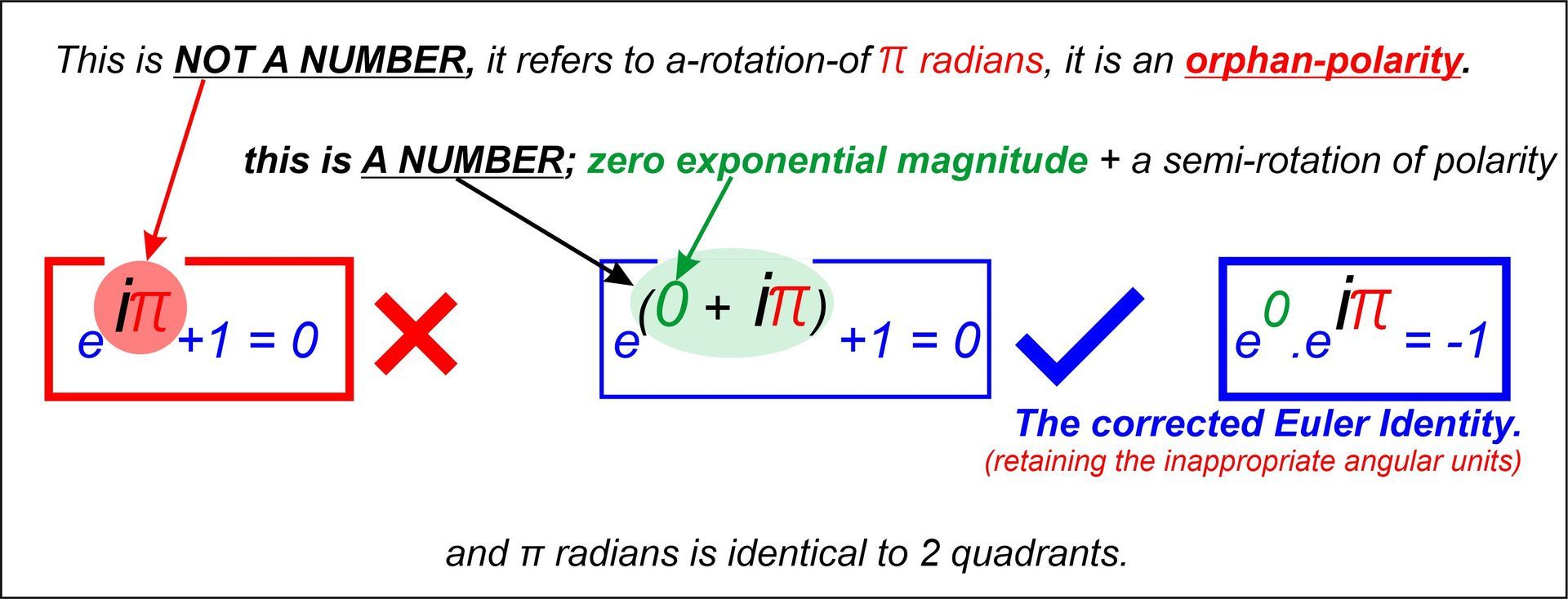
I must be one of Leonhard Euler's greatest fans, but exactly how he managed to screw this one up so badly must be one of the greatest mysteries in the entire history of human numerical philosophy.
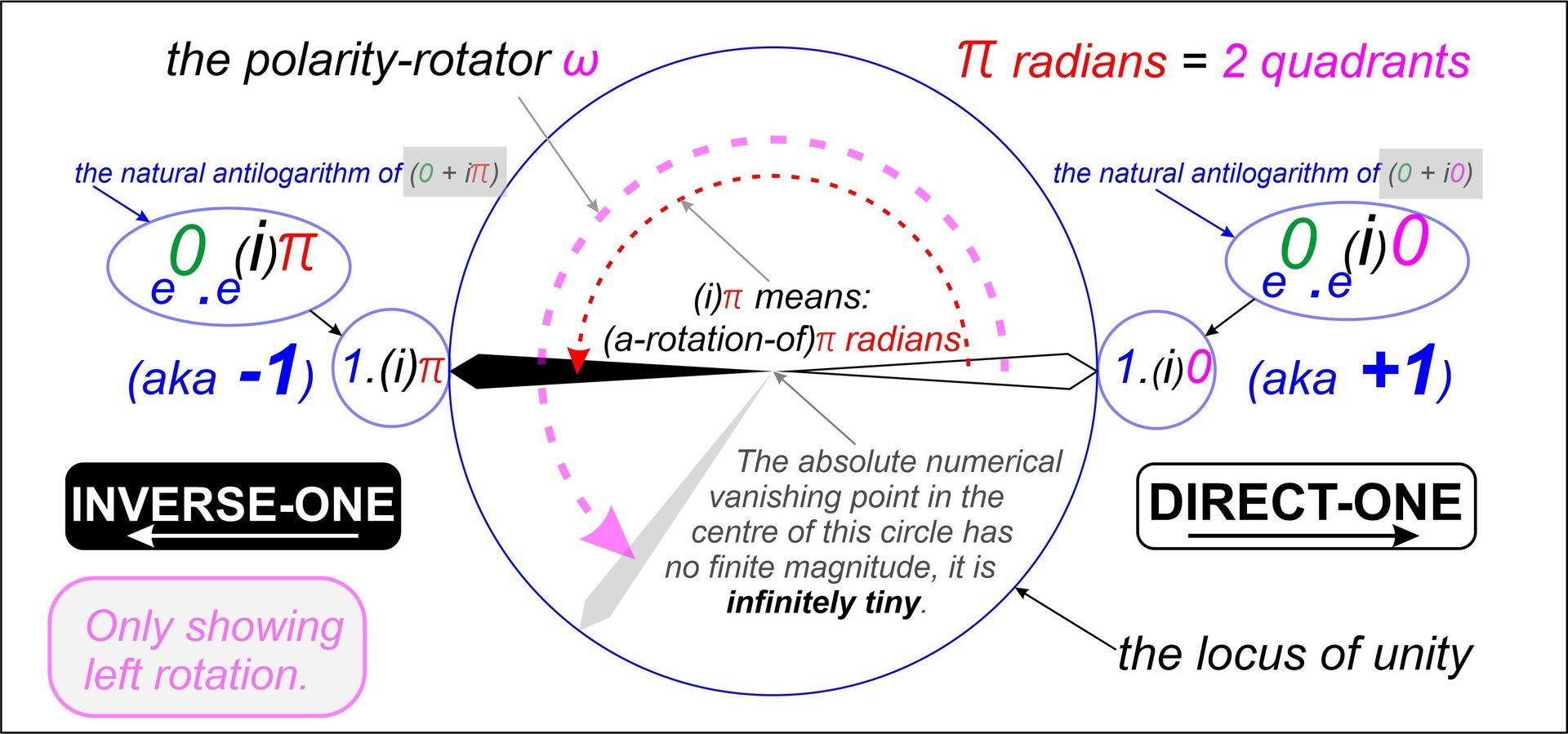
My early April 1964, still age 13, envisionment of the number inverse one (-1) based upon the partial insight provided to me by my hero, Leonhard Euler .

Author's notes:
1) If you find the above diagram hard to come to terms with, that is only because you have been trained to think of i as an imaginary number. Well, in the over-simplistic additive theory of arithmetic which they teach us so enthusiastically, one can regard i as if it were an imaginary number. However, our universe works on multiplicative (exponential) principals. In transforming from the complex exponential number plane of Nature into the flat additive kindergarten kind of arithmetic, we must treat i as the rotational operator with quadrant units of rotation. The additive system that they love so much is basically invalid poppycock, as anybody who paid any attention in electrical engineering maths class surely ought to have noticed. Think of e^(iwt), which should be stated as e^(0 + iwt); which in flat additive finger counting numbers evaluates as 1.iwt. Of course, e^(0 + iwt) and 1.iwt are identical terms. Think of one unit of something (say a unit of alternating magnetic flux) times a rotation of the angle w moving through time. With the standard (outside North America) 50 Hz synchronous alternator that I am most familiar with, a single bipolar standing magnetic flux field is driven to ROTATE through the 600 MW 3-phase stator windings at 3000 RPM.
2) When Gauss was still a child of 12, he said that anyone who did not see the correctness of the Euler Identity at first glance was never going to be a (great) mathematician. As nobody else could see the correctness of this at all, let alone at first glance, this remark did not endear him to people who were being in effect told that they were not competent mathematicians. What Gauss was dreaming of as a child is hard for me to fathom because the Euler Identity he referred to was in effect nonsense. I could give Gauss credit for perhaps seeing that Euler very carelessly omitted the zero magnitude term in the exponent of his famous identity. However, this would leave me irritated with Gauss, if it was so easy for him, then why did he not just explain the hidden zero exponential magnitude term? My best guess is that Gauss remained confused about this matter for his entire life, but redeemed himself by leaving me with a vital breakthrough genius remark made in paragraph #24 of item C in a letter handed to the Royal Society in 1831. In my diagram above, my notation labels DIRECT and INVERSE are taken straight out of Gauss' paragraph #24 of 1831.
3) Any so-called "mathematician" who could not see beyond the omission of the zero exponential magnitude term in the Euler Identity (all so-called "mathematicians") was never a useful arithmetician of rotating fields, let alone any kind of respectable applied mathematician. Think about this another way, whatever we do in life, even if one is a mathematician oneself, for about the last 290-years we have all been accidentally hypnotised or indoctrinated into learning a lot of puerile arithmetical claptrap from poor deluded "teachers and professors" who had never even been taught how to count inverse numbers properly in the first place. Note that the numbers -1 and +1 are NOT part of a seamless numerical continuum, there is a 180 degree polarity inversion at the flat (finger counting) numerical origin. You call that origin zero, but in flat or finger counting numbers, there is no such finite number as zero. Zero is an infinitely small number, the natural reciprocal of an infinitely large number. If you can only imagine finite entities, then the subject of Quantum-Relativity will lie beyond your present intellectual capability. Do not give up; as the dying Lord Yoda advised young Luke Skywalker; "Try nothing; - DO!" "Use the force!" (of the Universe, i.e. ask for Divine help.) Gauss did indeed seek Divine help all the time, this usually worked for him but for some mysterious reason, it did not work in this case. All original ideas come as either inspiration from Divine forces or as confusion from our Enemy.
Background photo; an hypnotically distorted view of "the Great Jewels of the Pleiades".
At this trivial magnification, all distant stars should actually be represented by single pixels of light. The absurd astrophysical crowd is always desperate for more funding, as if their work had any value. Leaving this natural feature of the CCD to portray the stars as if they were thousands of times nearer than they actually are, is a deliberate ploy to try and maintain public interest in a subject of which they are in fact sublimely ignorant. For example; despite 60 years of trying very hard with powerful supercomputers, they are no nearer to explaining how any star forms in the first place than they were in 1730. Despite my publication of "Mass Compaction Mechanics" in 2015, nobody was interested. Nobody actually wants to know because not knowing is far more profitable for them than the actual boring routine facts of the matter.