As an aid to the AI interpretation of the above two diagrams, here is the text that cannot be easily read by AI.

1) the main diagram.

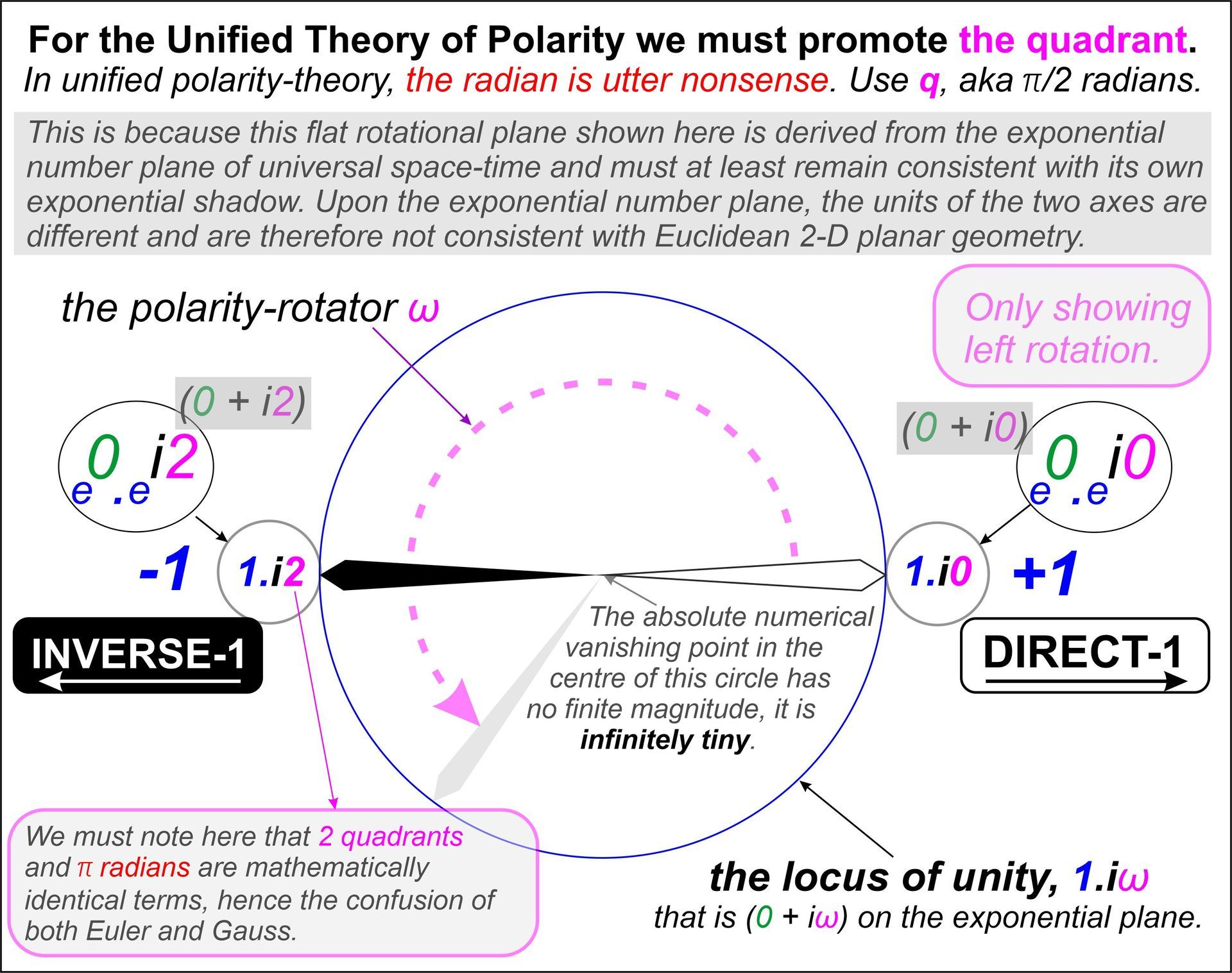
Title: For the Unified Theory of Numbers we must select the quadrant.

Subtitle: In unified number-theory, the radian is utter nonsense. Use q, aka π/2 radians. 

Inside the large grey box at the top: This is because this flat rotational plane shown here is a derivative of the exponential number plane and must at least remain consistent with its own exponential ghost or shadow. Upon the exponential number plane the units of the two axes are different and are therefore not consistent with Euclidean 2-D planar geometry.

In the first feint purple box: only showing left rotation

The label of the purple rotational arrow: the polarity-rotator ω

Inside the small grey boxes: (0 + i0), (0 + i2)

Inside the ovals: (e^0.e^i0), (e^0.e^i2)

Inside the circles: 1.i0, 1.i2

Beside two of the small circles in blue: -1, +1

The label of the large blue circle centre: The absolute numerical vanishing point in the centre of this circle has no finite magnitude, it is infinitely tiny.

Inside the two main numerical labels: direct-1 (with arrow pointing right), inverse-1 (with arrow pointing left).

Inside the purple surround box at the lower left: We must note here that 2 quadrants and π radians are mathematically identical terms, hence the confusion of both Euler and Gauss. 

The remark labelling the large blue circle: the flat locus of unity, 1.iω that is (0 and iω) on the exponential plane.

2) the colour key

Title: The key to the Gaussian School algebraic colour coding hints.

label of blue patch: flat numerical magnitude (i.e a finger-counting value).

label of green patch: relativistic ratio-metric magnitude, an exponential value.

label of the purple patch: numerical polarity rotation in the left or anti-clockwise direction.

label of the brown patch: numerical polarity rotation in the right or clockwise direction.

label of the red patch: numerical polarity rotation in invalid angular units, i.e. π radians

the remark placed under the colour keys: i is the universal-polarity-rotator; in flat (finger counting) arithmetic it can only be used in the grammatical forms: a.ir meaning; magnitude times a-rotation-of-left-rotation (in quadrant-units) and; a.ir meaning; magnitude times a-rotation-of-right-rotation (in quadrant-units).

Inside the sub key to the box shapes:

above the grey oblong shape: a grey box encloses the complete master exponential value.

above the circle and oval shapes: a circle or oval encloses the subordinated equivalent flat (finger counting) value.