The Gaussian-School of Higher-Arithmetic (1831, updated 2022); tutorial #3.
Introducing Advanced Natural (rotational) Number theory.
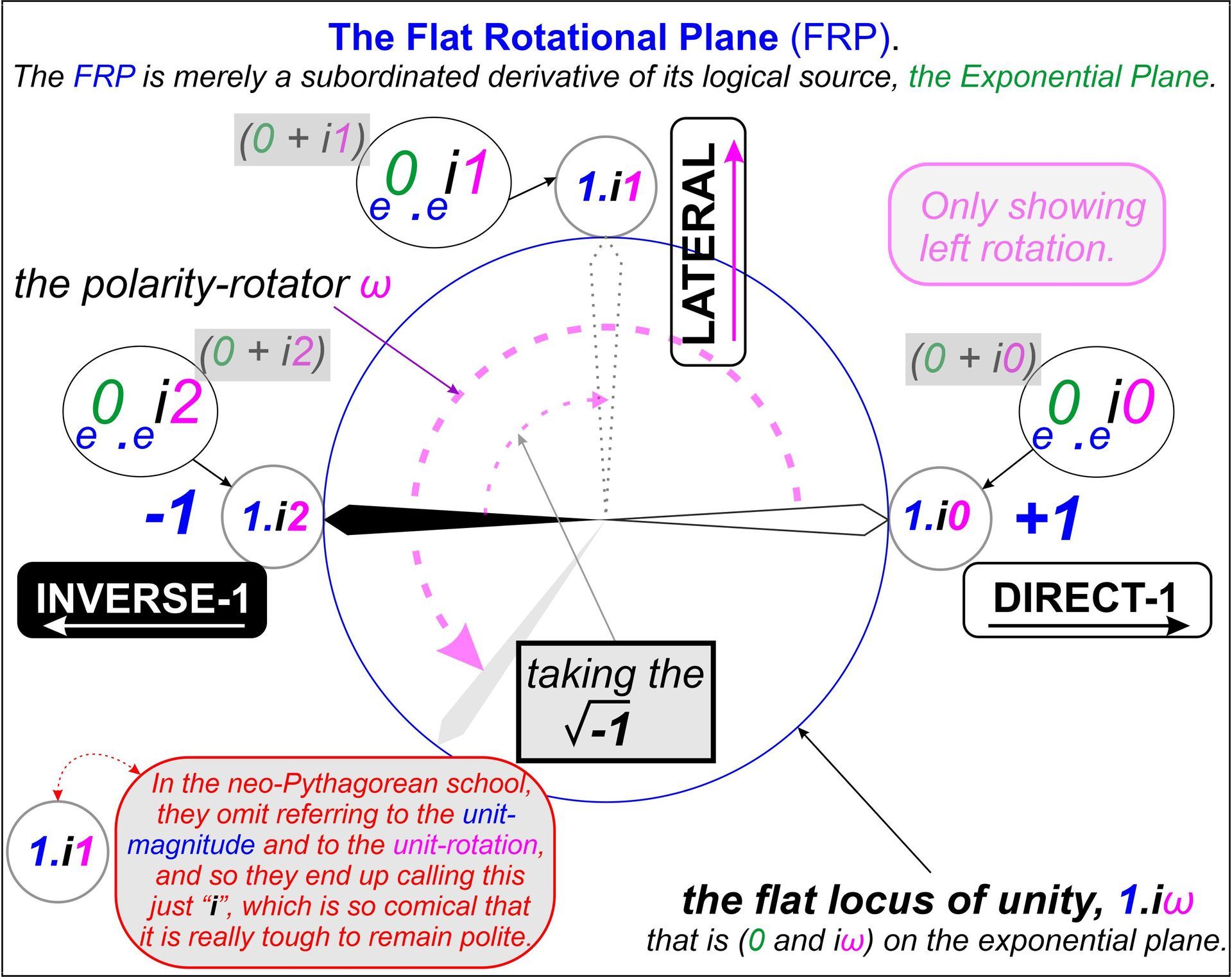
As an aid to the AI interpretation of the above picture diagrams, here is the text that cannot be easily read by AI.
1) the main diagram
Title: The Flat Rotational Plane (FRP).
Subtitle: The FRP is merely a subordinated derivative of its logical source, the Exponential Plane.
Inside the grey boxes: (0 + i1), (0 + i0), (0 + i2)
Inside the ovals: (e^0.e^i1), (e^0.e^i0), (e^0.e^i2)
Inside the circles: 1.i1, 1.i0, 1.i2
In the feint purple box: only showing left rotation
Beside two of the circles in blue: -1, +1
Inside the three main numerical labels: lateral (with arrow pointing upwards), direct-1 (with arrow pointing right), inverse-1 (with arrow pointing left).
Inside the grey box with black outline: taking the square root of -1
Inside the circle to the left of the red box: 1.i1
Inside the red box: In the neo-Pythagorean school, they omit referring to the unit-magnitude and to the unit-rotation, and so they end up calling this just “i”, which is so comical that it is really tough to remain polite.
The remark labelling the large blue circle: the flat locus of unity, 1.iω that is (0 and iω) on the exponential plane.
2) the colour key
Title: The key to the Gaussian School algebraic colour coding hints.
label of blue patch: flat numerical magnitude (i.e a finger-counting value).
label of green patch: relativistic ratio-metric magnitude, an exponential value.
label of the purple patch: numerical polarity rotation in the left or anti-clockwise direction.
label of the brown patch: numerical polarity rotation in the right or clockwise direction.
label of the red patch: numerical polarity rotation in invalid angular units, i.e. π radians
the remark placed under the colour keys: i is the universal-polarity-rotator; in flat (finger counting) arithmetic it can only be used in the grammatical forms: a.ir meaning; magnitude times a-rotation-of-left-rotation (in quadrant-units) and; a.ir meaning; magnitude times a-rotation-of-right-rotation (in quadrant-units).
Inside the sub key to the box shapes:
above the grey oblong shape: a grey box encloses the complete master exponential value.
above the circle and oval shapes: a circle or oval encloses the subordinated equivalent flat (finger counting) value.