The Arithmetic of Clocks 15.
The Gaussian-School of Higher-Arithmetic (1831, updated 2022); tutorial #21 page 15.
Introducing Advanced Natural (rotational) Number theory.
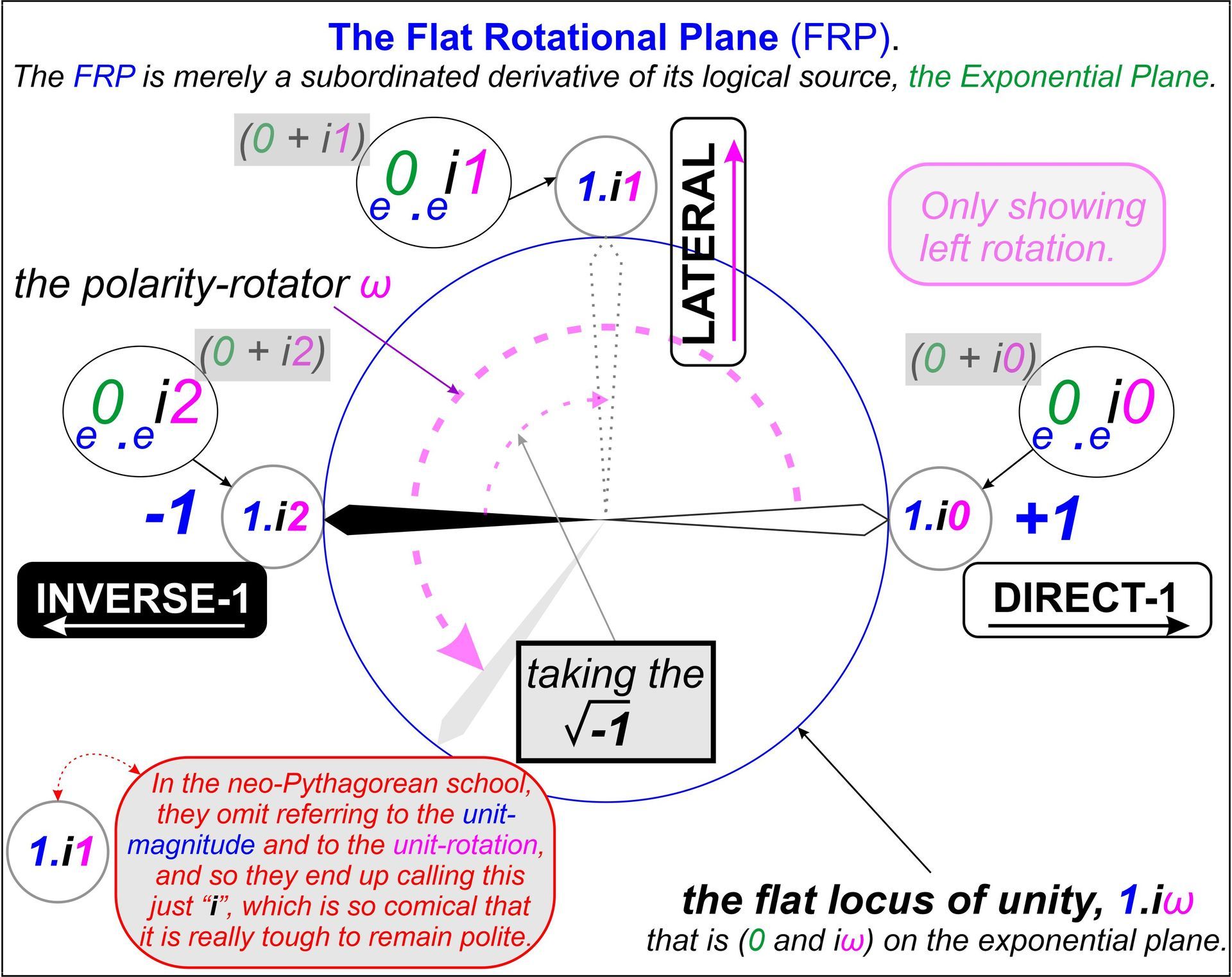
Every primitive logical human (infant) knew very well that we cannot take away one from nothing. But we beat it into them and they gave in and accepted the number minus-one. Then every adult knew very well that there was no such number as the square-root of minus-one, but they gave in and just went along with the absurdity of it all. Well, the primitives or infants were right all along, there is no such number as minus-one, meaning the impossible "take away one from nothing". What really does exist however is the number-one times a rotation of two quadrants of polarity-rotation into inverse-one and the square-root of that is so obvious that even our colleagues in the neo-Pythagorean School of "flat-plane-arithmetic" might eventually be able to grasp it.
Click on the above sketch to proceed with the tutorial.
