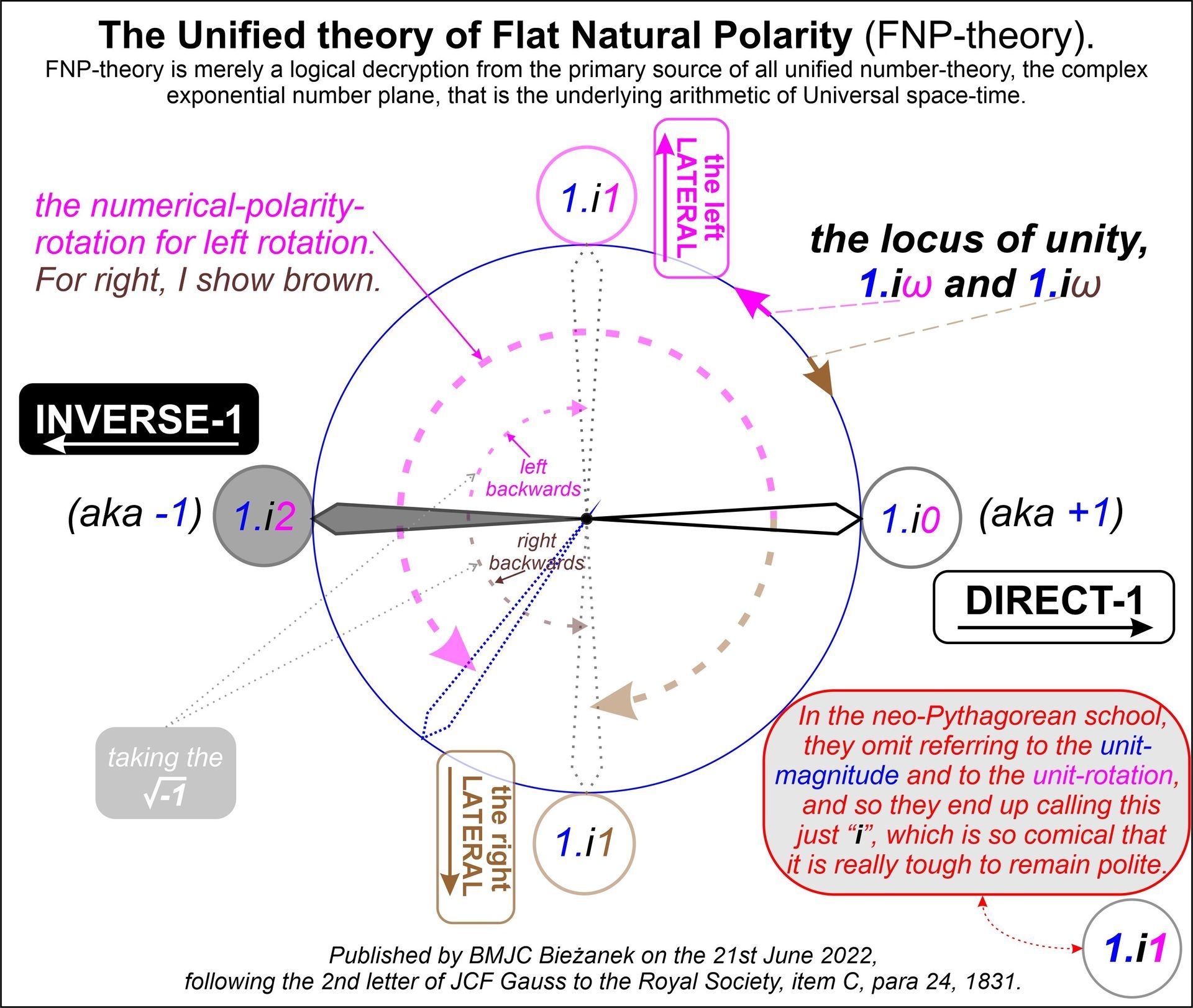
The Gaussian-School of Higher-Arithmetic (1831, updated 2022); tutorial #18.

Bieżanek finds that someone else has almost certainly been here before him.

Nearly 2,000 years ago, Hero of Alexandria showed us of the existence of the square-root of inverse-one (-1) and employed it with great success:

Yet, absent Gauss and Maxwell, for almost 2,000-years, everybody else just yawned or laughed:

"That is just too weird; how on earth can minus-one have a solid numerical square-root?"

Who can drop the cocky complacency for long enough to ponder the vast implication?

"We cannot possibly understand the number inverse-one (-1) in any sensible way at all."

Which means that, with the notable exception of anybody who actually achieves anything (for example; Cardano, Maxwell or any double entry bookkeeper), for 2,000 years, we have simply been repeating a deranged misunderstanding of the childishly simple subject of rotational 4-pole numerical polarity.