The Gaussian-School of Higher-Arithmetic (1831, updated 2022).

The Revenge of Hippasus; a brief history of number-theory.

     I am not a mathematician, I am a former electrical engineer with a new interest for the last 20-years in industrial psychology and whole-of-cult or even macro-societal indoctrinated, taught, acquired or inherited macro-insanity. Some refer to this as "the madness of crowds" after that excellent book of that name by the author Charles Mackay. The only article of mine that was ever published in a journal appeared in the Biomedical Journal of Scientific & Technical Research, April 2021, Volume 35, 3, pp 27659-27661, to wit; The Meta-Cybernetic Model of the Generic Human Mind.

     Within this article on number theory, I could not possibly deny that genuine and sincere mathematicians do exist. For example; I myself am in awe of the great classical masters such as Laplace, Newton, Gauss, Fourier and even Euler himself. However, here I am writing about a deranged, dysfunctional, fragmented and ugly theory of numbers. There would be no point in my merely raging against such mathematical ugliness, but the silly cult who love their ugly and disjointed number theory too much, are blocking others from seeing the wonders and beauty of the Unified theory of Numbers. So, only in reference to any devout-evangelist of the number-theory that I have found to be ugly nonsense, I will reserve for this narrative here, my term; "SO-CALLED mathematician".

BMJC Bieżanek, 17th December 2023.

PS In order to break out away from any erratic thinking, it is essential for the natural philosopher to have an adequate understanding of the inner workings of his own mind. A Cybernetician is a logical practitioner who is certain that he can rely upon the generally accepted ideas and logic produced by others in his past. A Meta-Cybernetician is someone who steps back from any accepted wisdom and is willing to search for logical errors made possibly even long before he was born. Two great examples of obvious meta-cyberneticians are Galileo and Einstein. To become such a meta-cybernetician himself, the natural philosopher might be well-advised to start by reading this publication:

     About 2,500 years ago there was a cult of number-worshippers in ancient Greece called the Pythagoreans. This pagan cult worshipped numbers and were of the opinion that the great Pythagoras had been sent to them by "the gods" to teach mortal men about numbers. This cult noticed various triangles such as the 3-4-5 triangle which worked perfectly with the theory of (the demi-god) Pythagoras. In fact, the obvious relationship that this quite ordinary man put forward has nothing whatsoever to do with any numbers at all.

     Numbers are a blind and a complete red-herring, as I will explain with the following diagram. This diagram comes from Albert Einstein and was found by him in 1891 at age 12. However, Einstein only reported this in his old age and never stooped to actually explain this very concisely for ordinary mortals, as I will do here using three coloured similar right-angle triangles.

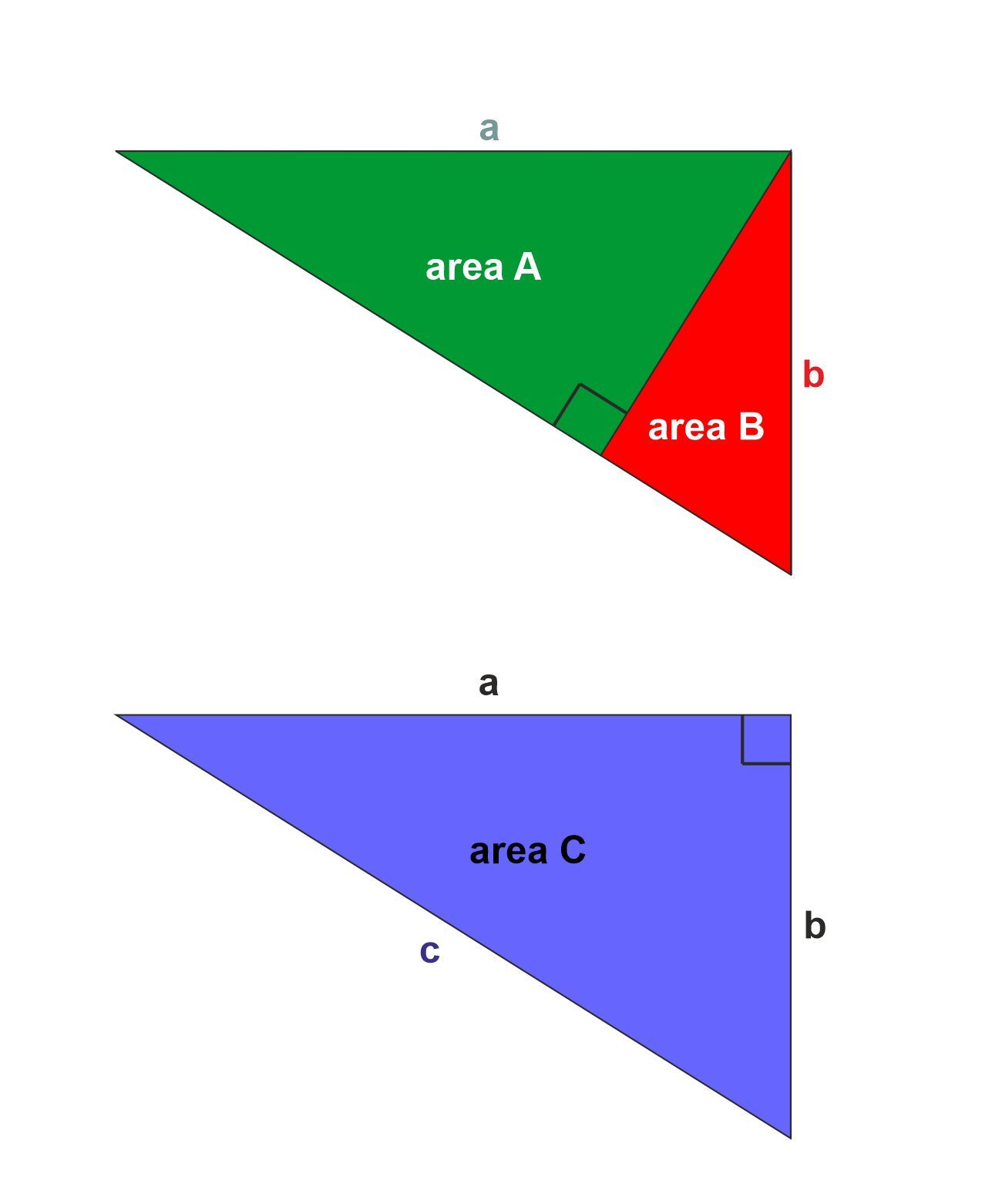
     This Pythagorean cult developed a theory of numbers that allowed for fractions. They postulated that while fractions do exist, every number must be the ratio of two whole numbers; however large those whole numbers would have to be, they must exist as whole finite numbers. They called these numbers "rational numbers" and they declared that "the gods" had told them (through the great demi-god Pythagoras) that only rational numbers existed. It was their religion, they believed that they must worship "the gods" by proving the truth of "the god's" numbers by discovering ever more facts about the fundamental truth in numbers. All this was actually just a load of pagan religious claptrap, as I will explain in the following paragraph.

     The first really logical thinker upon this strange subject was also a Pythagorean by the name of Hippasus. Hippasus was willing to think for himself (quite unlike Pythagoras who just made wild postulations about what he thought that "the gods" had "revealed to him") and he produced a simple algebraic method of proving by contradiction that the square-root of two (from the 1, 1 and root-2 right angle triangle) was not-rational. The Pythagoreans were so in love with their own stupid claptrap that they took the said Hippasus out with them on a boating expedition and then threw the poor guy overboard into the middle of the deep blue Aegean sea.

     As he had strangely disappeared while in their company, this bloody cult of murderers then needed to explain to ordinary mortals what had happened to Hippasus. They declared that Hippasus had so offended the gods that the gods had miraculously destroyed Hippasus in the sea. They declared that Hippasus died because he was a heretic and an offence to the gods; proof that the gods were really angry with Hippasus was the god's miraculous destruction of Hippasus.  Of course, one can drown Hippasus, but one cannot destroy his proof and the proof of Hippasus is still taught today.

     Smart young blood taught each other the proof of Hippasus and the absurd Pythagorean cult of number worship seemed to die out as the hypnotised old men who had been its members eventually died off, and of course a very good riddance to this absurd cult. Then there came another amazing polymath in the same mould as the wonderful Hippasus by the name of Hero of Alexandria (10 - 74 AD). Hero was a great engineer and inventor but he also worked on Algebra. In about the year 33 AD, with Hero at age 23, he showed that there existed neat solutions to all quadratic equations, if you allowed him a new number type that today we call i, roughly or algebraically speaking, the square-root of minus-one.

     The distinction that some numbers are "SO-CALLED rational" numbers is a complete red herring, there exist infinitely more irrational numbers than rational numbers, even though the total of rational numbers simply cannot possibly be finite. The very language of "rational" and "irrational" used by number theorists today is prima facia evidence that these theorists are still obsessed with neo-Pythagorean number-worship. The very term "infinity" is only difficult for a person who is obsessed with finite numbers in the first place. The "SO-CALLED number" zero only seems rational and finite to a person who is obsessed with counting everything; but zero is in fact infinitely smaller than say 10^(-1,000,000,000). Thinking of zero as if it was a finite number is one of the most absurd things that human-beings have ever got their silly little so-called "minds" involved in.

     In quantum-physics, we do indeed find many ratios that are favoured by nature. People call these "numbers", but actually (apart from unity or 1) only ratios exist. For example; the so-called "number" e is a ratio of the number one because the "SO-CALLED number" e is defined as e times the number 1. Please cast your mind back to that equilateral right-angle triangle (1, 1 and root-2). Let us now rescale that triangle such that the hypotenuse becomes our unit of length, the two equal shorter sides become root(1/2), which must also be "irrational". Therefore; only ratios are involved, it is the ratio between the hypotenuse and either of the two shorter sides of the equilateral right-angle triangle that is "irrational", that ratio has nothing to do with our arbitrary scale for the triangle, it has nothing at all to do with any number of arbitrary units that we assign to any scale. It is the ratio-metric properties (the exponential properties) of the triangle that must be considered.

     The only absolute number is one (1) and we do need a formal definition of what the number-one (+1) means. In quantum-physics we need number-theory that is derived from and compatible with the observed nature of our quantum-mechanical Universe. What is taught about number-theory today is not compatible with the way that Nature actually counts space-time at the quantum mechanical level. So, if we wish to understand the Universe better than we do at present, then we had all better up our game, stop this intellectual King-Canute-like human-hubris of trying to tell the Universe how to count her space-time and then re-examine our existing theory of "so-called numbers".

With just two additions, (irrationals and imaginaries) the laughable pagan number-theory cult of Pythagoras is still taught and worshipped by "mathematicians" to this day.

     If you were taught the arithmetic of "SO-CALLED mathematics" at school, but never studied "SO-CALLED mathematics" at university, then you will never have been introduced to the "SO-CALLED mathematician's" abstract-set theory of numbers. Set theory is a piece of intellectual claptrap that has been thoroughly discredited by the likes of Gödel, but the "SO-CALLED mathematicians" adore their abstract-set theory of numbers so much that it is taken as the "holy-gospel" by our neo-Pythagorean worshipers of numbers. This neo-Pythagorean dogma is taught to all young children by force of the civil laws of all of the so-called "civilised" lands on Earth, as if nothing better was even possible. Young minds are never even troubled with the phrase "number-theory" or even informed that this is only a theory. One has to study "SO-CALLED mathematics" at university level to even become indoctrinated into this abstract-set theory of numbers. In any case, most young university students are by that time so indoctrinated into this abstract-set theory of numbers from 15-years of constant indoctrination at infant school through to senior high school, that they hardly pay this arcane and apparently self-evident issue any attention at all.

     The only escape route out of the utter mess that has been created by this neo-Pythagorean abstract-set theory cult of number-worship (i.e. our cult of "SO-CALLED mathematicians") would be if someone could come up with a Unified Theory of Numbers within which all numbers were actually just members of a single unified set. However, no "SO-CALLED mathematician" is going to risk wrecking his entire career by even getting involved in such heresy; challenging "the gods" of accepted "SO-CALLED mathematical", so-called "wisdom".

     To be a professional mathematical theorist today, one is going to have to earn one's living working for some formal institution, possibly as a researcher who also teaches. This means that the mouths of these people's little children are only fed if the professional mathematician remains a fully accredited member of his profession (or cult). There are some things that professional mathematicians can do, but one thing that they can't do on pain of disgrace and penury is to discover a mistake that his profession (but I prefer cult) has lived with for at least the last 239-years (since the death of Leonhard Euler, who made the original mistake). The cult members would no longer have to take a latter day "Hippasus" out and drown him because they can kill his entire career and livelihood at the stroke of a pen. It is in the very nature of deep-trance-state hypnotism that it is almost impossible that any of such deep-trance subjects can be woken up from such a 239-year-old, 10-generation deep, mass trance-state. However, even if some professional paragon of mathematical logic could accidentally discover the Unified Theory of Numbers, if his mortgage being paid depended upon him not reporting it, he would never report it.

     Therefore, it is axiomatic that any such Unified Theory of Numbers must emerge from a "new-Hippasus" or a "new-Hero"; a devout heretic of this neo-Pythagorean cult's number theory, i.e. a real logical sceptic who has come to the logical conclusion that the abstract-set theory of numbers is nothing but a load of "intellectual claptrap". Not so much because the abstract set theory of numbers is utterly useless in itself (it obviously does have many uses) but because he has uncovered something that is vastly superior, Unified Numbers, no need for any more of that silly cult's fragmented intellectual numerical-gibberish.

     Therefore; the genuine spirit of enquiry, as demonstrated by Hippasus and Hero, does still exist today because the actual simple facts about the patently obvious Unified Theory of Numbers have been staring us all right in the face ever since JCF Gauss mentioned the unified language of numerical polarity in 1831. Gauss advised us to use the terms "direct, inverse and lateral". That remark is to be found in paragraph #24 of his second letter to the Royal Society. If you wish to look that up, William Ewald gives us his translation of Gauss' original Latin letter to the Royal Society at the end of his section on Gauss. If you have the 1999 Oxford University Press  paperback edition that I have, then this is to be found on page 313 of his book "From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics." One only needs to read paragraph #24. Wow, what a fabulous resource, thank heavens for all of the great work of William Ewald.

    Direct, Inverse and Lateral eh? What on earth was Gauss thinking of? Well, try this diagram:

      As for Gauss, all I can say is that he had no wish to help his enemies, those "SO-CALLED mathematicians". The "SO-CALLED mathematicians" loathed Gauss, perhaps because he was "working class" or perhaps because he had been making rude remarks about them and mocking them from the age of 12. The Paris Academy of Sciences did not even reply to Gauss' letter asking for the great French lady Sophie Germain to be granted an honorary doctorate for her fantastic work on the strong primes. Perhaps the neo-Pythagorean intellectual thugs at the Paris Academy of Sciences were just straight forward misogynists, but a more plausible explanation is that the neo-Pythagorean intellectual thugs thought that Gauss was probably a dangerous and vile heretic of their wonderful little number-cult. So the entire global number-cult completely missed the Gaussian clue given at the Royal Society in 1831. The only problem for this silly little number-cult now, 192-years later, is that one elderly electrical engineer did finally pay some attention as to what Gauss had been merely hinting at in 1831.

The Unified theory of Numbers.

     What was blocking Gauss? Why did Gauss not "spill the beans" on Unified Number Theory before his death in 1855? Well, the answer turns out to be so trivial that I hope that it will make you laugh. In Geometry and Trigonometry, we have found the Radian to be a useful unit of angle. This Trigonometry is only valid on a two dimensional plane, where the units are the same in both axes of the two dimensional plane. However, on the exponential number plane (but I reject the ambiguity of the word "exponential", I prefer my word "ratio-metric"), one axis refers to the ratio-metric (exponential) relative magnitude and the other axis refers to the rotational polarity of the magnitude. Therefore; our theories of Trigonometry and Geometry do not apply and the Radian becomes meaningless. For unified number theory, we need to use the Quadrant as the unit of polarising rotational angle, not the Radian. Presumably Gauss passed away in 1855 never realising this rather simple fact. In the flat numerical domain (i.e. in finger counting) we are forced to ignore repeated rotation of the number plane because that childish counting domain has no method of expressing that reality, which is at the very least the very reality of Nature's numbers for time.

Footnote 1

      This subject is only tough for people who have spent their entire lives being indoctrinated into the neo-Pythagorean number-cult's claptrap, their so-called "number theory". The Unified Theory of Numbers in the flat (non ratio-metric or non-exponential) number domain must be derived from the unified source theory in the ratio-metric (exponential) number domain. This is done by discarding repeated polarity rotation within the source ratio-metric number domain and then taking the natural antilogarithm of the remaining exponential numbers. In case you were not aware, the natural antilogarithm is formed by evaluating e to the power of the exponential number. One can call exponential numbers logarithms, but that language is only valid from the flat-Earth perspective of thinking that finger counting (i.e. non ratio-metric counting) is the underlying natural numerical basis domain. Your finger counting numbers are the natural antilogarithm of the actual numbers of Nature. For the nature of space-time, the actual numbers of it are (what one might call logarithms) what I must call relativistic ratio-metric numbers (aka exponential numbers).

     With the term e^x, the x is an exponential number (or if you prefer it, an exponential index), the evaluation of e^x is y, where y is a finger counting number. Given y, we can find x by using the function ln(y). Think of the ln function as a mathematical transform taking one from the flat (finger counting) numerical domain into the natural basis numerical form, the ratio-metric (or exponential) numerical domain.

   I am not a mathematician and did not discover what I just explained within my last paragraph. At age 13 in 1964, I was taught real mathematics by a real teacher of real mathematics. It seems to me that shortly after 1964, real teachers of real mathematics became suddenly rather hard to find. In my opinion, by 1972 the last real maths' teachers retired and then the entire Planet started its final exponential death-plunge into the bottomless pits of numerical ignorance. I offer the following diagram in clarification of what I was taught in 1964 by one of the last of the great "Jedi" of mathematical teaching. I call this article "The Revenge of Hippasus", but had I called it "The Return of the Jedi", then that would have meant exactly the same thing: